Decision Tree 決策樹 #
決策樹,顧名思義,是用一個樹狀的模型做決策。如下圖,便是一個決定是否要帶傘的決策樹。
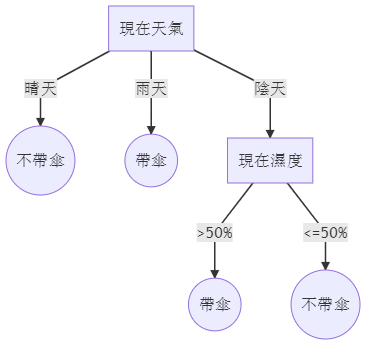
決策樹可以多種方式實作,其中常見的一種實作方式:Classification and Regression Trees 或簡稱 CART,是由 Breiman, Friedman, Olshen, and Stone 等人發表的演算法在 1984 年所發表的演算法。如名稱所述,可以同時處理分類問題與迴歸問題。
優點是模型具有很高的可解釋性,很容易知道為什麼魔行會做出這樣的預測。很方便地處理類別特徵以及缺失值。缺點是難以學習到特徵之間的加法關係。
迴歸樹 Regression Tree #
雖然一般的決策樹沒有限制一個節點可以分出幾個子節點,不過在 CART,每次只切成兩個節點。
令我們的資料 \( D = \{\bold{x_n},y_n\}_{n=1}^N, where\;\bold{x_n}\in\R^p,y_n \in\R \) ,為一個有 N 筆資料,p 維特徵,一維實數 label 的迴歸問題資料集。
模型可以寫成數學式如下:
\[f(x)=\Sigma_{m=1}^M c_m I(x\in R_m)\]我們這顆樹有 \(M\) 個葉子 \( R_m \) , \( c_m \) 是葉子 \(m\) 的預測值。 \(I\) 是 indicator function,若 \(x\) 落在葉子 \(m\) 則值為 1,否則為 0。
我們現在要最佳化 square error \( \Sigma(y_i - f(x_i))^2 \) ,那最好的 \( c_m \) 很明顯就是所有落在葉子 \(m\) 的 label \(y\) 平均: \( \hat{c_m}= \Sigma_{x_i\in R_m}\frac{y_i}{|R_m|} \) (公式一),其中 \( |R_m| \) 為被分到 \( R_m \) 中的資料筆數。
從所有資料開始,我們要在第 \(j\) 維切在 \(s\) 上,意思是 \( x_j \le s \) 的資料分一到一個子樹,剩下的分在令一個子樹。我們使用貪心的做法,對每一個節點,我們要找出最好的 \(j\) 跟 \(s\) ,然後遞迴下去。
\[\min_{j,s} [\min_{c_1} \Sigma_{x_i\in R_1(j,s)}(y_i-c_1)^2 + \min_{c_2} \Sigma_{x_i\in R_2(j,s)}(y_i-c_2)^2]\]由公式一可知,最好的 \( \hat{c_1}= average(y_i | x_i \in R_1(j,s)) \) , \( c_2 \) 同理。對每個特徵 \(j\) ,枚舉所有可能的 \(s\) 便可以算出要在哪裡切出子節點。由這個方式一直遞迴下去直到每個葉子對應到一筆訓練資料,便可以做到完美的 training error,很明顯的 overfitting,所以我們必須對樹做剪枝。
剪枝 Pruning #
把樹建多大可以是遞迴時限制最深深度、每個葉子至少要有幾筆資料、或是每次 error 必須下降多少等等。但因為我們是使用貪心法切割節點,所以這種做法通常會讓訓練的 error 很差,令一個做法是樹建完(不一定要建到每個葉子對應到一筆訓練資料,可以是對應十筆,樹不要太小就好)以後再做剪枝。
剪枝可以使用以下方法:
\[\min_P Error(T_P) + \alpha |T_p|\]策略 \(P\) 是把節點合併的方法(子樹合併為一個葉子), \( T_p \) 是合併後的樹,找出 mean square error 跟 \( |T_p| \) (樹的大小)中的權衡,其中 \( \alpha \) 是參數。給定 \( \alpha \) ,我們可以使用 weak link pruning:每次找到合併後 error 變高最小的節點,一直到只剩一個節點為止,從這之中得到最好的合併策略 \(P\) 。而 \( \alpha \) 可以由 cross validation 決定。
分類樹 Classification Tree #
在迴歸樹時,我們的預測值是一個實數,在分類樹我們的預測值就是一個類別。
在迴歸樹時我們最佳化訓練資料的 square error。我們定義 \( p_{mk} \) 為節點 \(m\) 中有 class \(k\) 的比例,其中 \(k\) 為比例最大的 class 。對於分類問題,有幾個可用的 impurity measure (衡量指標):
- 錯誤率: \( 1-p_{mk} \)
- Gini index: \( \Sigma_{k=1}^K p_{mk}(1-p_{mk}) \)
- Cross entropy: \( -\Sigma_{k=1}^K p_{mk}\log(p_{mk}) \)
其中 Gini index 與 Cross entropy 比錯誤率更加常用。
類別特徵 Categorical Feature #
在處理數值特徵時,如果該特徵只有 \(q\) 個值,那我們只有 \(q-1\) 種切法。但如果是類別特徵,會有 \( 2^{q-1}-1 \) 種切法。在分類樹只有兩個 class 的情況下,我們可以將類別轉換成該類別 label 為 1 的比例,然後當成數值特徵處理,在使用 Cross entropy 或是 Gini index 的情況下這種切法是最佳的。在迴歸樹使用 square error 的情況下將類別轉換成該類別 label 的平均也可以達到最佳。但是在 multi-class classification 下,並沒有這種性質,只能使用近似演算法。
缺失值 Missing Value #
比起其他模型處理缺失值時可能會給與一個猜測的數值,基於樹的模型有更好的處理方法:使用「替代」(surrogate)的特徵。
在對特徵 \(j\) 計算切點的時候先忽略缺值的資料,然後使用另外的特徵 \(j'\) ,找出最好的分割點讓分割後的結果最像原本 \(j\) 切出來的結果。如果 \(j'\) 還是有很多缺值,可以使用第三個特徵 \(j''\) ,找出 \(j''\) 上最好的分割點讓分割後的結果為全部第二像原本 \(j\) 切出來的結果,等等。如果找不到其他特徵時,則將缺值的特徵分到資料比較多的子節點。
Scikit Learn 套件 #
Scikit Learn 提供決策樹的實作,可以很方便使用分類樹與迴歸樹:
安裝:
pip install scikit-learn
使用:
from sklearn.tree import DecisionTreeClassifier, DecisionTreeRegressor
# classification tree
X = [[0, 0], [2, 2]]
y = [1, 0]
clf = DecisionTreeClassifier()
clf.fit(X, y)
print(clf.predict([[1, 1]]))
# regression tree
X = [[0, 0], [2, 2]]
y = [0.5, 2.5]
clf = DecisionTreeRegressor()
clf.fit(X, y)
print(clf.predict([[1, 1]]))
其中建議至少搜尋一下 max_depth 參數(樹的最大深度),如果處理 imbalance data 的話建議調整一下 class_weight (可以直接設成 balanced)。
參考資料:
The Elements of Statistical Learning §9.2 Tree-Based Methods